Summary of Statistics & Optimization (2021)
Published:
My 2021 paper reading list in statistics & optimization, with special emphasis on Bayesian method, sparse optimization and general LASSO problem.
Paper List
An augmented ADMM algorithm with application to the generalized lasso problem (2017, Journal of Computational and Graphical Statistics)
本文是对经典ADMM方法的改进方法。具体来说,本文提出了新的变罚形式来加速ADMM算法,可以在保持相同收敛速度的同时降低计算量。提出的aug-ADMM可以解决广义LASSO问题,即
\[\underset{\beta \in \mathbb{R}^{p}}{\operatorname{minimize}}(1 / 2) \cdot\|y-X \beta\|_{2}^{2}+\lambda\|A \beta\|_{1}.\]Preliminary:
考虑如下形式的优化问题:
\[\operatorname{minimize}_{\theta \in \mathbb{R}^{p}} f(\theta)+g(A \theta), \tag{1}\]其中$f(\cdot)$和$g(\cdot)$都是“简单”的凸函数,且$A\in \mathbb{R}^{m\times p}$。标准的ADMM算法首先通过引入等价约束$A \theta=\gamma$来解耦上述优化问题中的两个函数,可得到一个等价的联合优化问题,为:
\[\operatorname{minimize}_{\theta \in \mathbb{R}^{p}, \gamma \in \mathbb{R}^{m}} f(\theta)+g(\gamma) \quad \text { subject to } A \theta-\gamma=0.\]通过分裂算子、交替优化变量,ADMM将原联合优化问题化为若干子问题,并对原变量$(\theta,\gamma)$和对应的对偶变量$\alpha$交替优化更新,得到如下更新公式:
\[\begin{aligned} \theta^{k+1} &=\underset{\theta \in \mathbb{R}^{p}}{\arg \min }\left(f(\theta)+\frac{\rho}{2}\left\|A \theta-\gamma^{k}+\rho^{-1} \alpha^{k}\right\|_{2}^{2}\right), \\ \gamma^{k+1} &=\underset{\gamma \in \mathbb{R}^{m}}{\arg \min }\left(g(\gamma)+\frac{\rho}{2}\left\|A \theta^{k+1}-\gamma+\rho^{-1} \alpha^{k}\right\|_{2}^{2}\right), \\ \alpha^{k+1} &=\alpha^{k}+\rho\left(A \theta^{k+1}-\gamma^{k+1}\right) . \end{aligned}\]其中,$\rho > 0$表示惩罚参数,该迭代过程的收敛速率为$O(1/k)$。
aug-ADMM框架:
然而,上述ADMM的$\theta$-更新过程偶尔会难以计算,特别是当$A$是非对角阵时。为了克服这个困难,作者提出引入“增广”变量$(\gamma, \tilde{\gamma})$,其中$\tilde{\gamma}=\left(D-A^{\top} A\right)^{1 / 2} \theta$,且$D \in \mathbb{R}^{p \times p}$满足$D \succeq A^{\top} A$。则我们可以得到问题(1)的另一个等价形式,如下:
\[\operatorname{minimize}_{\theta, \tilde{\gamma} \in \mathbb{R}^{,}, \gamma \in \mathbb{R}^{m}} f(\theta)+g(\gamma), \\ \text { subject to }\left(\begin{array}{c} A \\ \left(D-A^{\top} A\right)^{1 / 2} \end{array}\right) \theta-\left(\begin{array}{l} \gamma \\ \tilde{\gamma} \end{array}\right)=0. \tag{2}\]对优化问题(2)利用标准的ADMM算法和简单化简,可以得到如下更新公式
\[\begin{aligned} \theta^{k+1} &=\underset{\theta \in \mathbb{R}^{p}}{\arg \min }\left(f(\theta)+\left(2 \alpha^{k}-\alpha^{k-1}\right)^{\top} A \theta+\frac{\rho}{2}\left(\theta-\theta^{k}\right)^{\top} D\left(\theta-\theta^{k}\right)\right), \\ \gamma^{k+1} &=\underset{\gamma \in \mathbb{R}^{m}}{\arg \min }\left(g(\gamma)+\frac{\rho}{2}\left\|A \theta^{k+1}-\gamma+\rho^{-1} \alpha^{k}\right\|_{2}^{2}\right), \\ \alpha^{k+1} &=\alpha^{k}+\rho\left(A \theta^{k+1}-\gamma^{k+1}\right). \end{aligned}\]可以看到,上述更新公式中不再设计增广变量$\tilde{\gamma}$。当$D = A^{\top} A$时,增广ADMM回退为标准的ADMM算法。aug-ADMM的主要优势是增加了算法的灵活性,即可自由选择$D$来简化$\theta$的更新。
aug-ADMM推导细节:
首先,我们对优化问题(2)利用标准的ADMM算法,可以得到若干子问题,其更新如下:
\[\theta^{k+1}= \underset{\theta \in \mathbb{R}^{p}}{\arg \min }\left(f(\theta)+\frac{\rho}{2}\left(\left\|A \theta-\gamma^{k}+\rho^{-1} \alpha^{k}\right\|_{2}^{2}\right.\right. \\ \left.\left.\quad+\left\|\left(D-A^{\top} A\right)^{1 / 2} \theta-\tilde{\gamma}^{k}+\rho^{-1} \tilde{\alpha}^{k}\right\|_{2}^{2}\right)\right), \tag{3a}\\\] \[\gamma^{k+1}=\underset{\gamma \in \mathbb{R}^{m}}{\arg \min }\left(g(\gamma)+\frac{\rho}{2}\left\|A \theta^{k+1}-\gamma+\rho^{-1} \alpha^{k}\right\|_{2}^{2}\right), \tag{3b}\] \[\tilde{\gamma}^{k+1}=\left(D-A^{\top} A\right)^{1 / 2} \theta^{k+1}+\rho^{-1} \tilde{\alpha}^{k}, \tag{3c}\] \[\alpha^{k+1}= \alpha^{k}+\rho\left(A \theta^{k+1}-\gamma^{k+1}\right), \tag{3d}\] \[\tilde{\alpha}^{k+1}=\tilde{\alpha}^{k}+\rho\left(\left(D-A^{\top} A\right)^{1 / 2} \theta^{k+1}-\tilde{\gamma}^{k+1}\right), \tag{3e}\]其中$\alpha\in \mathbb{R}^m$和$\tilde{\alpha}\in \mathbb{R}^p$均表示相关的对偶变量。
然后,结合(3c)和(3e),可以得到$\tilde{\alpha}^{k+1}=0$。再将(3c)代入(3a)中,$\theta$的更新过程可以化简为
\[\theta^{k+1}=\underset{\theta \in \mathbb{R}^{p}}{\arg \min }\left(f(\theta)+\frac{\rho}{2}\left(\left\|A \theta-\gamma^{k}+\rho^{-1} \alpha^{k}\right\|_{2}^{2}+\left\|\left(D-A^{\top} A\right)^{1 / 2}\left(\theta-\theta^{k}\right)\right\|_{2}^{2}\right)\right). \tag{4}\]接着,结合式(3d),可以得到$\theta$的最终更新公式:
\[\theta^{k+1} =\underset{\theta \in \mathbb{R}^{p}}{\arg \min }\left(f(\theta)+\left(2 \alpha^{k}-\alpha^{k-1}\right)^{\top} A \theta+\frac{\rho}{2}\left(\theta-\theta^{k}\right)^{\top} D\left(\theta-\theta^{k}\right)\right).\]aug-ADMM的进一步简化(没看懂):
同时,结合(3b)和(3d),可以得到
\[\rho^{-1} \alpha^{k+1}=\rho^{-1} \alpha^{k}+A \theta^{k+1}-\operatorname{prox}_{\rho^{-1} g(\cdot)}\left(\rho^{-1} \alpha^{k}+A \theta^{k+1}\right).\]然后,结合Moreau’s identity,可以将$\alpha$的更新公式简化为
\[\alpha^{k+1}=\operatorname{prox}_{\rho g^{*}(\cdot)}\left(\alpha^{k}+\rho A \theta^{k+1}\right).\]注1:Moreau’s identity建立了关于$\Omega(\cdot)$的近端映射和其共轭函数$\Omega^{*}(\cdot)$的关系,即对任意的$t>0$,有
\[u=\operatorname{prox}_{t \Omega(\cdot)}(u)+t \operatorname{prox}_{t^{-1} \Omega^{*}(\cdot)}\left(t^{-1} u\right),\]其中近端映射定义为
\[\operatorname{prox}_{\Omega(\cdot)}(u)=\underset{v}{\arg \min }\left(\Omega(v)+\frac{1}{2}\|u-v\|_{2}^{2}\right),\]且共轭函数定义为
\[\Omega^{*}(v):=\sup _{u}\langle u, v\rangle-\Omega(u),\]它为凸函数。关于aug-ADMM的收敛性质在此不做详述(不懂)。
注2:文中关于$D$的选择建议为$D=\delta I$,其中$\delta \ge |A|^2$。
aug-ADMM的实验结果:
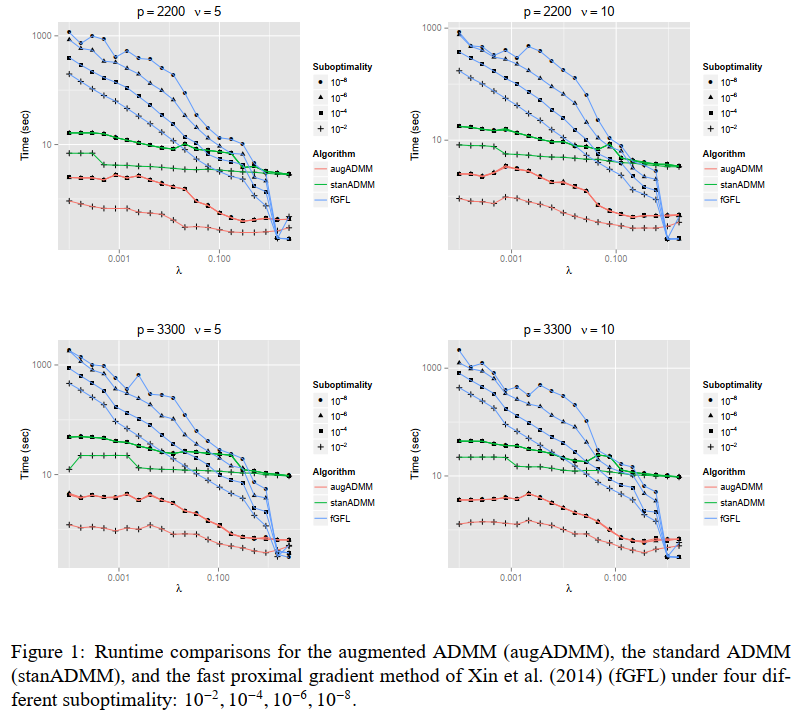
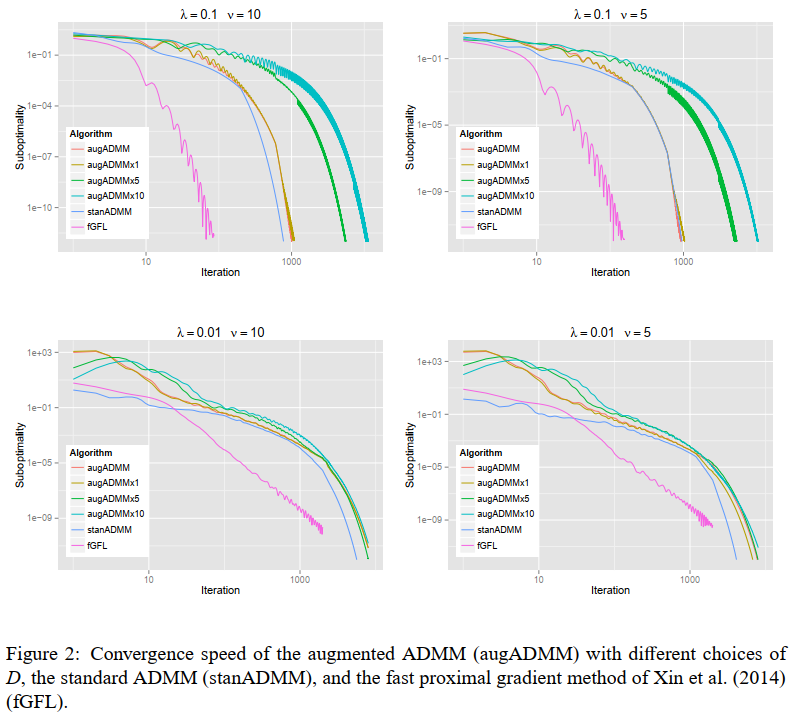
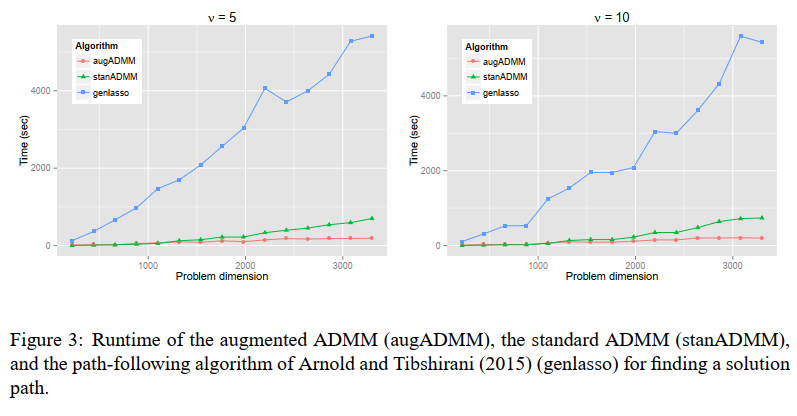

The solution path of the generalized lasso (2011, The Annals of Statistics)
广义LASSO问题可以被描述为:
\[\underset{\beta \in \mathbb{R}^{p}}{\operatorname{minimize}} \frac{1}{2}\|y-X \beta\|_{2}^{2}+\lambda\|D \beta\|_{1}, \tag{5}\]其中$\lambda \ge 0$表示稀疏参数,$D\in \mathbb{R}^{m\times p}$表示特定的惩罚矩阵,1-范数约束代表了结构稀疏约束。
主要学习了文章中“何时一个广义LASSO问题退化为LASSSO问题”部分,即”3. When does a generalized lasso problem reduce to a lasso problem”。
情况1: 矩阵$D$可逆
首先,如果$D$是一个$p\times p$维的可逆矩阵,那么,我们可以直接引入变量$\theta = D\beta$,结合矩阵的可逆性将(5)转换为LASSO问题,如下:
\[\underset{\theta \in \mathbb{R}^{p}}{\operatorname{minimize}} \frac{1}{2}\left\|y-X D^{-1} \theta\right\|_{2}^{2}+\lambda\|\theta\|_{1}.\]情况2: 矩阵$D$不可逆但行满秩
更一般地,如果$D$是一个$m\times p$维的矩阵且$rank(D)=m$(暗含$m\le p$),则我们仍然可以通过变量替换的方式将问题(5)转换为一个LASSO问题。
首先,我们可以构造一个$(p-m)\times p$维的矩阵$A$,它的行与$D$的每一行正交,从而构造一个$p\times p$维的满秩矩阵$\widetilde{D}=\left[\begin{array}{l}D \ A\end{array}\right]$,即$rank(\widetilde{D})=p$。然后,我们可以将变量转换为$\theta = (\theta_1,\theta_2)^T=\widetilde{D}\beta$,使得广义LASSO问题(2)变换为
\[\operatorname{minimize}_{\theta \in \mathbb{R}^{p}} \frac{1}{2}\left\|y-X \widetilde{D}^{-1} \theta\right\|_{2}^{2}+\lambda\left\|\theta_{1}\right\|_{1}. \tag{6}\]可以注意到(6)除了一范数约束只对变量$\theta$的部分变量$\theta_1$进行约束外,这基本上是一个一般的LASSO问题。
接下来,引入符号$X \widetilde{D}^{-1} \theta=X_{1} \theta_{1}+X_{2} \theta_{2}$;然后我们可以发现,对于$\theta_2$,这是一个最小二乘问题:
\[\operatorname{minimize}_{\theta_2 \in \mathbb{R}^{p}} \frac{1}{2}\left\|y-X_{1} \theta_{1}+X_{2} \theta_{2}\right\|_{2}^{2},\]即
\[\hat{\theta}_{2}=\left(X_{2}^{T} X_{2}\right)^{-1} X_{2}^{T}\left(y-X_{1} \hat{\theta}_{1}\right) .\]进一步地,我们可以将问题(6)重写为
\[\operatorname{minimize}_{\theta_{1} \in \mathbb{R}^{m}} \frac{1}{2}\left\|(I-P) y-(I-P) X_{1} \theta_{1}\right\|_{2}^{2}+\lambda\left\|\theta_{1}\right\|_{1}, \tag{7}\]其中$P=X_{2}^{T}\left(X_{2}^{T} X_{2}\right)^{-1} X_{2}^{T}$。利用算法,如LARS,ADMM对LASSO问题(7)进行求解后,可以得到原始广义LASSO问题的解:
\[\hat{\beta}=\widetilde{D}^{-1} \hat{\theta}.\]