Summary of Model-Driven Deep Learning (2022)
Published:
My 2022 paper reading list in model-driven deep learning.
模型启发的深度学习首先要需要基于问题背景,对任务进行数学建模。然后基于这个数学模型,设计一个合适的优化算法。一般来说,所选择或设计的优化算法是迭代算法。那么,我们可以将这个迭代算法展开为一个固定深度的神经网络,并通过数据驱动,让网络参数得以学习更新,即由模型启发而设计的深度网络。

参考PPT(2021.08.17组会):Model-driven deep learning —— differentiable programming。
Paper List
ADMM-CSNet: A deep learning approach for image compressive sensing (2018, TPAMI)
DeepWave: a recurrent neural-network for real-time acoustic imaging (2019, NIPS)
Learning fast approximations of sparse coding (2010, ICML)
本文用神经网络来学习稀疏编码问题。稀疏编码问题可以建模为一范数约束下的最小二乘问题,如下:
\[\boldsymbol{Z}^{*}=\underset{\boldsymbol{Z}}{\operatorname{argmin}} \frac{1}{2}\left\|\boldsymbol{X}-\boldsymbol{W}_{d} \boldsymbol{Z}\right\|_{2}^{2}+\alpha\|\boldsymbol{Z}\|_{1},\]其中$\boldsymbol{W}_{d}$表示字典矩阵。对于此优化问题,已有很多算法用于求解它,比如ISTA算法(见参考文献[7])。但ISTA算法为迭代算法,需要很多轮迭代才能收敛,计算成本是昂贵的,具体算法步骤如下:

作者注意到迭代算法,如ISTA,可以等价为一个循环神经网络,如下:
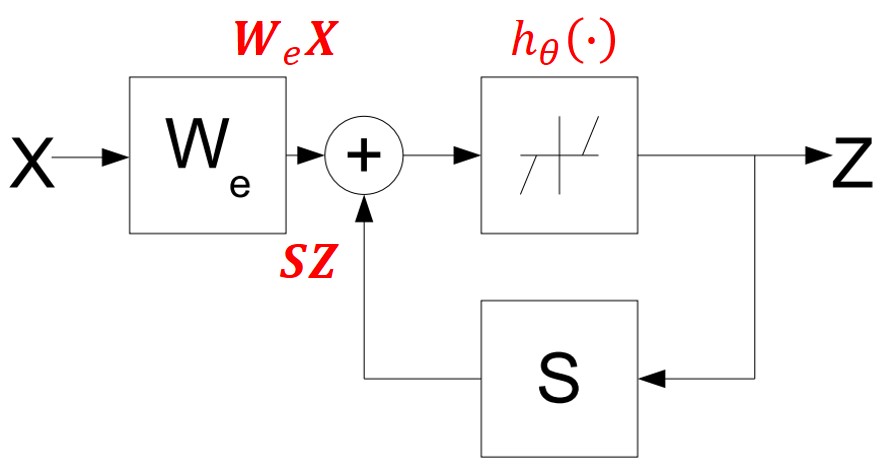
但这个网络是不断循环直至收敛的,这样的网络无法进行训练。那我们如何将ISTA算法转化为一个可训练的神经网络呢?作者提出,我们只需要将上图进行固定轮数的截断,就可以得到一个ISTA版本的神经网络,它等价于执行ISTA算法中的L轮迭代(其中L为网络的深度)。具体来说,本文提出的LISTA网络可以表示为如下形式:

其中$\boldsymbol{W}_{e}$, $\boldsymbol{S}$和$\theta$都是可学习的参数。至于损失函数,只需要最小化网络输出的稀疏编码与ground truth的稀疏编码即可,具体如下:
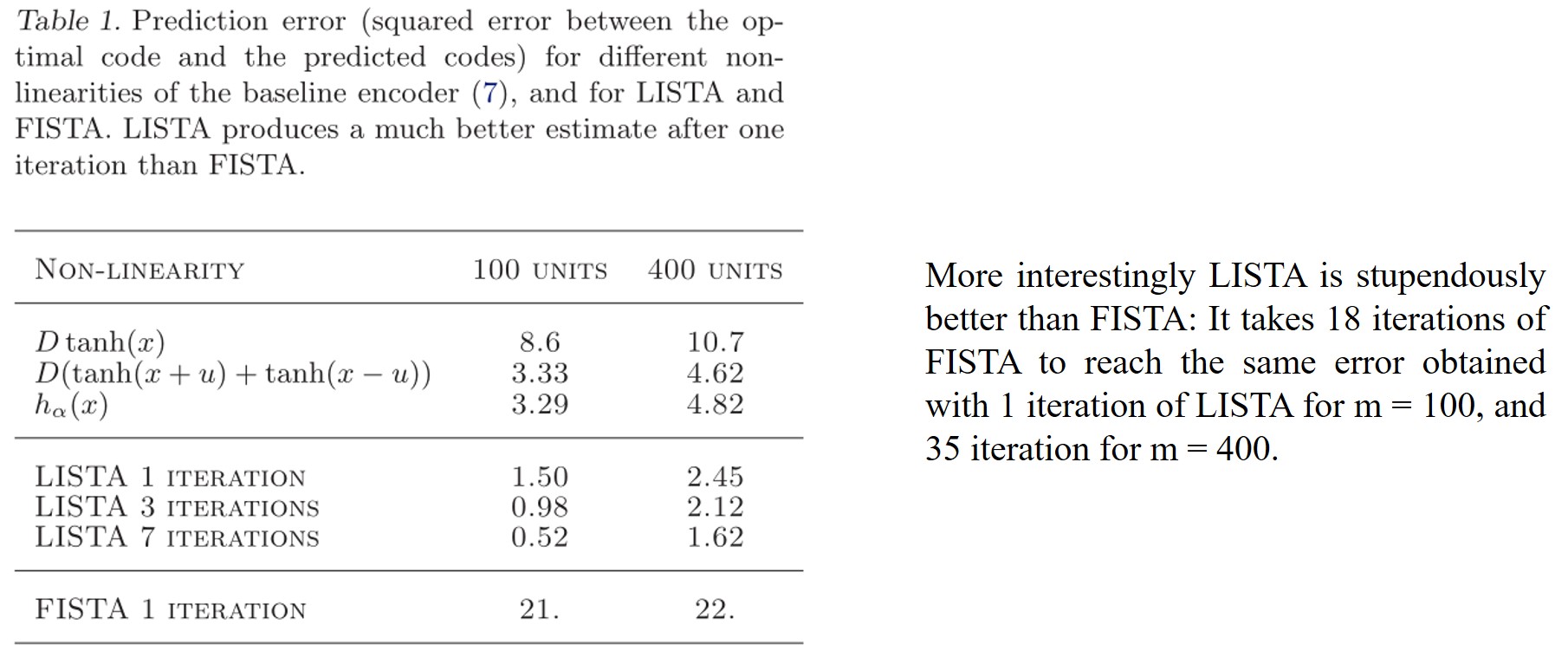
\[\begin{aligned} &L(\boldsymbol{W})=\frac{1}{P} \sum_{p=1}^{P} L\left(\boldsymbol{W}, \boldsymbol{X}^{p}\right) \text { with } \\ &L\left(\boldsymbol{W}, \boldsymbol{X}^{p}\right)=\frac{1}{2}\left\|\boldsymbol{Z}^{* p}-f_{e}\left(\boldsymbol{W}, \boldsymbol{X}^{p}\right)\right\|_{2}^{2}. \end{aligned}\]网络可以很好取得较小估计误差和较快的运行时间。部分数值实验结果截取如下:
Deep ADMM-Net for compressive sensing MRI (2016, NIPS)
本文用ADMM启发的深度网络来解决MRI压缩感知的问题。作者发现了传统方法和深度学习方法中的问题:
传统方法:最佳变换域以及稀疏约束的选择难以确定,并且难以确定最优参数(如稀疏参数、步长参数等),同时算法需要上百轮迭代才可以收敛;
深度学习方法:CNN计算高效,但感受野有限;DNN感受野深,但计算慢。同时深度学习的黑盒属性让网络难以自动学习变换的稀疏性。
压缩感知MRI模型可以描述如下:

而ADMM算法(见参考文献[8])是解决这个问题的一个有效方案,ADMM通过迭代优化三个子问题来求解上述优化问题,此即:
\[\left\{\begin{array}{l} \boldsymbol{x}^{(n+1)}=\underset{\boldsymbol{x}}{\operatorname{argmin}} \frac{1}{2}\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{y}\|_{2}^{2}-\sum_{l=1}^{L}\left\langle\boldsymbol{\alpha}_{l}^{(n)}, \mathbf{z}_{l}^{(n)}-\boldsymbol{D}_{l} x\right\rangle+\sum_{l=1}^{L} \frac{\rho_{l}}{2}\left\|\mathbf{z}_{l}^{(n)}-\boldsymbol{D}_{l} \boldsymbol{x}\right\|_{2}^{2}, \\ \boldsymbol{z}^{(n+1)}=\underset{\boldsymbol{z}}{\operatorname{argmin}} \sum_{l=1}^{L} \lambda_{l} g\left(\mathbf{z}_{l}\right)-\sum_{l=1}^{L}\left\langle\boldsymbol{\alpha}_{l}^{(n)}, \mathbf{z}_{l}-\boldsymbol{D}_{l} \boldsymbol{x}^{(n+1)}\right\rangle+\sum_{l=1}^{L} \frac{\rho_{l}}{2}\left\|\mathbf{z}_{l}-\boldsymbol{D}_{l} \boldsymbol{x}^{(n+1)}\right\|_{2}^{2}, \\ \boldsymbol{\alpha}^{(n+1)}=\underset{\boldsymbol{\alpha}}{\operatorname{argmin}} \sum_{l=1}^{L}\left\langle\boldsymbol{\alpha}_{l}, \boldsymbol{D}_{l} \boldsymbol{x}^{(n+1)}-\boldsymbol{z}_{l}^{(n+1)}\right\rangle. \end{array}\right.\]上述子问题可以等价写作:
\[\left\{\begin{array}{l} \mathbf{X}^{(\mathbf{n})}: \boldsymbol{x}^{(n)}=\boldsymbol{F}^{T}\left[\boldsymbol{P}^{T} \boldsymbol{P}+\sum_{l=1}^{L} \rho_{l} \boldsymbol{F} \boldsymbol{D}_{l}^{T} \boldsymbol{D}_{l} \boldsymbol{F}^{T}\right]^{-1}\left[\boldsymbol{P}^{T} \boldsymbol{y}+\sum_{l=1}^{L} \rho_{l} \boldsymbol{F} \boldsymbol{D}_{l}^{T}\left(\mathbf{z}_{l}^{(n-1)}-\boldsymbol{\beta}_{l}^{(n-1)}\right)\right], \\ \mathbf{Z}^{(\mathbf{n})}: \mathbf{z}_{l}^{(n)}=S\left(\boldsymbol{D}_{l} x^{(n)}+\boldsymbol{\beta}_{l}^{(n-1)} ; \lambda_{l} / \rho_{l}\right), \\ \mathbf{M}^{(\mathbf{n})}: \boldsymbol{\beta}_{l}^{(n)}=\boldsymbol{\beta}_{l}^{(n-1)}+\eta_{l}\left(\boldsymbol{D}_{l} \boldsymbol{x}^{(n)}-\mathbf{z}_{l}^{(n)}\right). \end{array}\right.\]注意到ADMM算法是不断迭代上述式子,得到最后的收敛解。那么,我们可以设计L层的深度网络,将算法的迭代步骤用于指导网络的设计。具体来说,ADMM-Net的stage n便对应于ADMM算法的第n轮迭代,网络架构如下:
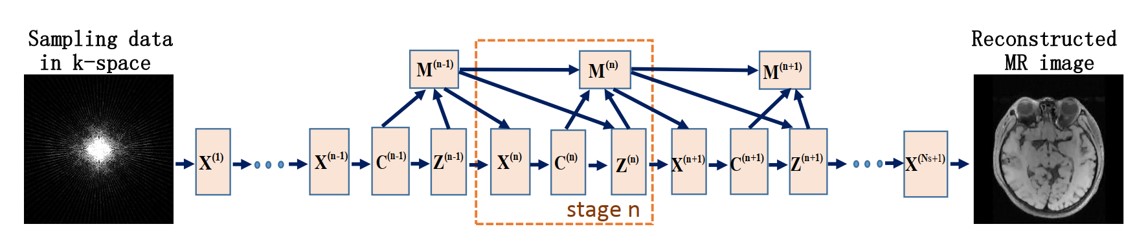
ADMM-Net网络中定义了四种操作,分别为:
1. Reconstruction operation $\boldsymbol{X}^{n}$
对应于ADMM中的:
\[\boldsymbol{x}^{(n)}=\boldsymbol{F}^{T}\left[\boldsymbol{P}^{T} \boldsymbol{P}+\sum_{l=1}^{L} \rho_{l} \boldsymbol{F} \boldsymbol{D}_{l}^{T} \boldsymbol{D}_{l} \boldsymbol{F}^{T}\right]^{-1}\left[\boldsymbol{P}^{T} \boldsymbol{y}+\sum_{l=1}^{L} \rho_{l} \boldsymbol{F} \boldsymbol{D}_{l}^{T}\left(\mathbf{z}_{l}^{(n-1)}-\boldsymbol{\beta}_{l}^{(n-1)}\right)\right].\]Deep ADMM-Net – Reconstruction layer:
\[\boldsymbol{x}^{(n)}=\boldsymbol{F}^{T}\left[\boldsymbol{P}^{T} \boldsymbol{P}+\sum_{l=1}^{L} \rho_{l} \boldsymbol{F} \boldsymbol{H}_{l}^{T} \boldsymbol{H}_{l} \boldsymbol{F}^{T}\right]^{-1}\left[\boldsymbol{P}^{T} \boldsymbol{y}+\sum_{l=1}^{L} \rho_{l} \boldsymbol{F} \boldsymbol{H}_{l}^{T}\left(\mathbf{z}_{l}^{(n-1)}-\boldsymbol{\beta}_{l}^{(n-1)}\right)\right],\]其中$\boldsymbol{H}_{l}$为第$l$个滤波器,是可学习的参数。
第一个stage的更新公式为:
\[\boldsymbol{x}^{(1)}=\boldsymbol{F}^{T}\left(\boldsymbol{P}^{T} \boldsymbol{P}+\sum_{l=1}^{L} \rho_{l}^{(1)} \boldsymbol{F} \boldsymbol{H}_{l}^{(1) T} \boldsymbol{H}_{l}^{(1)} \boldsymbol{F}^{T}\right)^{-1}\left(\boldsymbol{P}^{T} \boldsymbol{y}\right).\]2. Convolution operation $\boldsymbol{C}^{n}$
对应于ADMM中的:
\[\mathbf{z}_{l}^{(n)}=S\left(\boldsymbol{D}_{l} x^{(n)}+\boldsymbol{\beta}_{l}^{(n-1)} ; \lambda_{l} / \rho_{l}\right).\]Deep ADMM-Net – Convolution layer:
\[\boldsymbol{c}_{l}^{(n)}=\boldsymbol{D}_{l}^{(n)} \boldsymbol{x}^{(n)},\]其中$\boldsymbol{D}_{l}^{(n)}$表示可学习的滤波矩阵。该操作是为了将图片变换到某个合适的变换域。
注:与ADMM算法不同,$H_{l}$,$D_{l}$ 没有被设置为两个不同的可学习矩阵,这是为了增加网络的学习能力。
3. Nonlinear transform operation $\boldsymbol{Z}^{n}$
对应于ADMM中的:
\[\mathbf{z}_{l}^{(n)}=S\left(\boldsymbol{D}_{l} x^{(n)}+\boldsymbol{\beta}_{l}^{(n-1)} ; \lambda_{l} / \rho_{l}\right).\]为了学习更灵活的变换,本文提出使用分段线性函数进行拟合,定义如下:
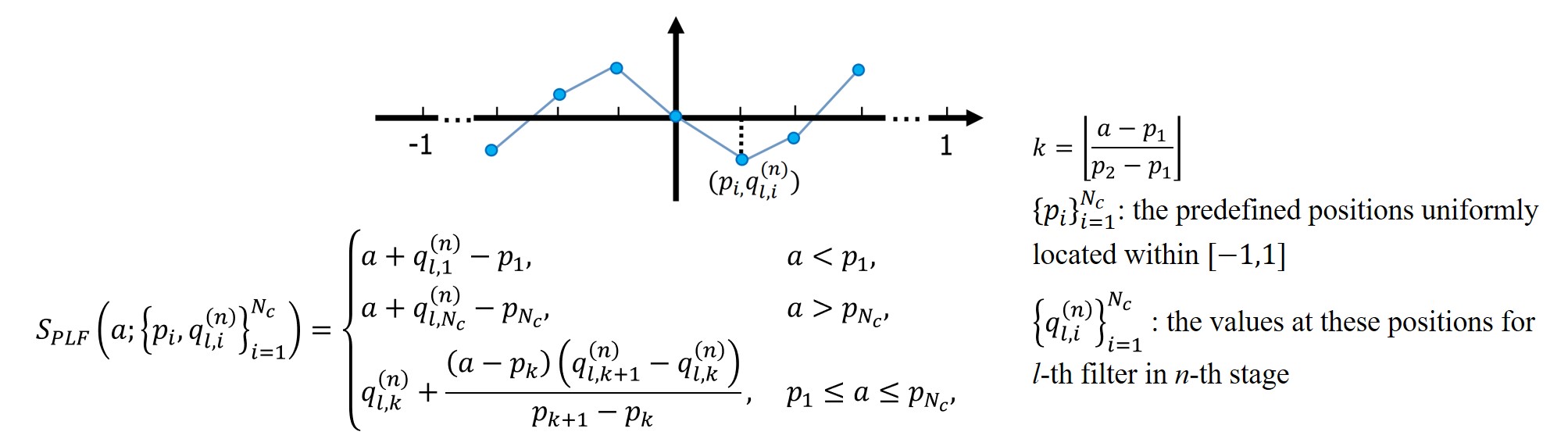
Deep ADMM-Net — Nonlinear transform layer :
\[\mathbf{z}_{l}^{(n)}=S_{P L F}\left(\boldsymbol{c}_{l}^{(n)}+\boldsymbol{\beta}_{l}^{(n-1)} ;\left\{p_{i}, q_{l, i}^{(n)}\right\}_{i=1}^{N_{c}}\right).\]4. Multiplier update operation $\boldsymbol{M}^{n}$
对应于ADMM中的:
\[\boldsymbol{\beta}_{l}^{(n)}=\boldsymbol{\beta}_{l}^{(n-1)}+\eta_{l}\left(\boldsymbol{D}_{l} \boldsymbol{x}^{(n)}-\mathbf{z}_{l}^{(n)}\right).\]Deep ADMM-Net — Multiplier update layer:
\[\boldsymbol{\beta}_{l}^{(n)}=\boldsymbol{\beta}_{l}^{(n-1)}+\eta_{l}^{(n)}\left(\boldsymbol{c}_{l}^{(n)}-\mathbf{z}_{l}^{(n)}\right),\]其中$\eta_{l}^{(n)}$表示可学习的参数。
网络的损失函数和可学习参数如下所示:

部分数值结果展示如下:
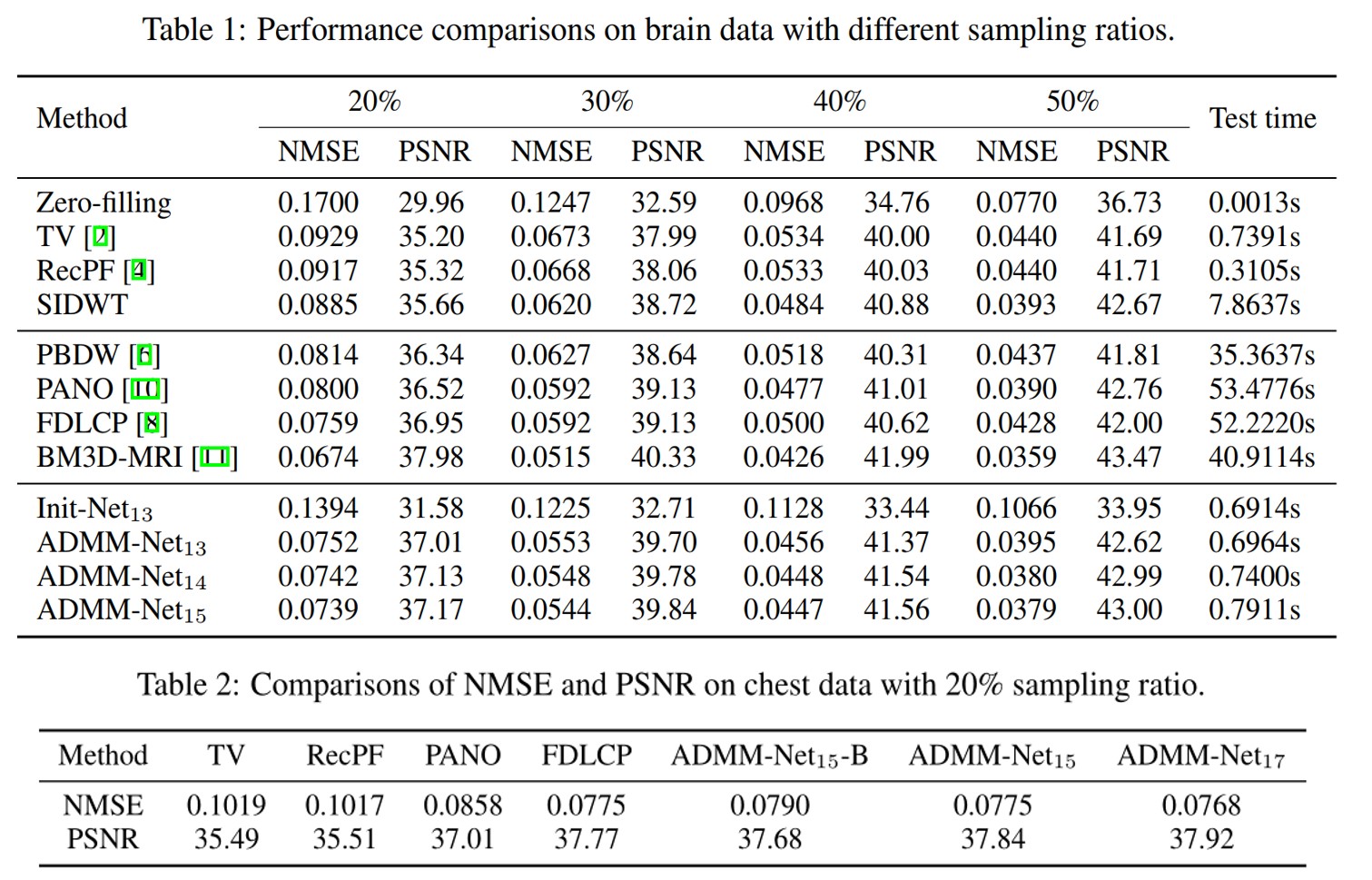
ADMM-CSNet: A deep learning approach for image compressive sensing (2018, TPAMI)
本文是对ADMM-Net的一个拓展。ADMM算法解决MRI压缩感知问题有两种方案,其中一种就是论文ADMM-Net的方案。而本文提出的ADMM-CSNet则是对ADMM另一种求解方案的网络化版本,区分如下:

具体由ADMM的另一种方案衍生出ADMM-CSNet网络的方法与ADMM-Net类似,在此不做详述。
ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing (2018, CVPR)
本文的主要贡献为:
提出了一种新颖的网络,即ISTA-Net,它采用ISTA更新步骤的结构来设计可学习的深度网络表现形式;
通过利用压缩感知领域的残差域知识,衍生出增强版$\text{ISTA-Net}^{+}$,以进一步提高网络性能;
用更有效和通用的方式解决了非线性稀疏变换相关的近端映射问题。
压缩感知问题可以被建模为:
\[\min _{\boldsymbol{x}} \frac{1}{2}\|\boldsymbol{\Phi} \mathbf{x}-\mathbf{y}\|_{2}^{2}+\lambda\|\Psi \mathbf{x}\|_{1}.\]而ISTA算法[7]的解决步骤可以总结为:
\[\begin{aligned} &\boldsymbol{r}^{(k)}=\boldsymbol{x}^{(k-1)}-\rho \boldsymbol{\Phi}^{\top}\left(\boldsymbol{\Phi} \boldsymbol{x}^{(k-1)}-\boldsymbol{y}\right), \\ &\boldsymbol{x}^{(k)}=\underset{\boldsymbol{x}}{\arg \min } \frac{1}{2}\left\|\boldsymbol{x}-\boldsymbol{r}^{(k)}\right\|_{2}^{2}+\lambda\|\boldsymbol{\Psi} \mathbf{x}\|_{1}, \end{aligned}\]其中第二个优化问题为近端优化问题,即
\[\operatorname{prox}_{\lambda \phi}(\boldsymbol{r})=\underset{x}{\operatorname{argmin}} \frac{1}{2}\|x-\boldsymbol{r}\|_{2}^{2}+\lambda \phi(\boldsymbol{x}).\]受CNN强大的拟合能力的启发,作者提出用两层带ReLU的CNN层来进行学习变换函数:$\mathcal{F}(\boldsymbol{x})=\boldsymbol{\Psi}$,则优化问题可以表示为:
\[\boldsymbol{x}^{(k)}=\underset{\boldsymbol{x}}{\arg \min } \frac{1}{2}\left\|\boldsymbol{x}-\boldsymbol{r}^{(k)}\right\|_{2}^{2}+\lambda\|\mathcal{F}(\boldsymbol{x})\|_{1}.\]ISTA-Net同样贯彻了模型启发的深度学习的思路,利用网络的phase来学习ISTA的迭代过程,具体网络架构如下:
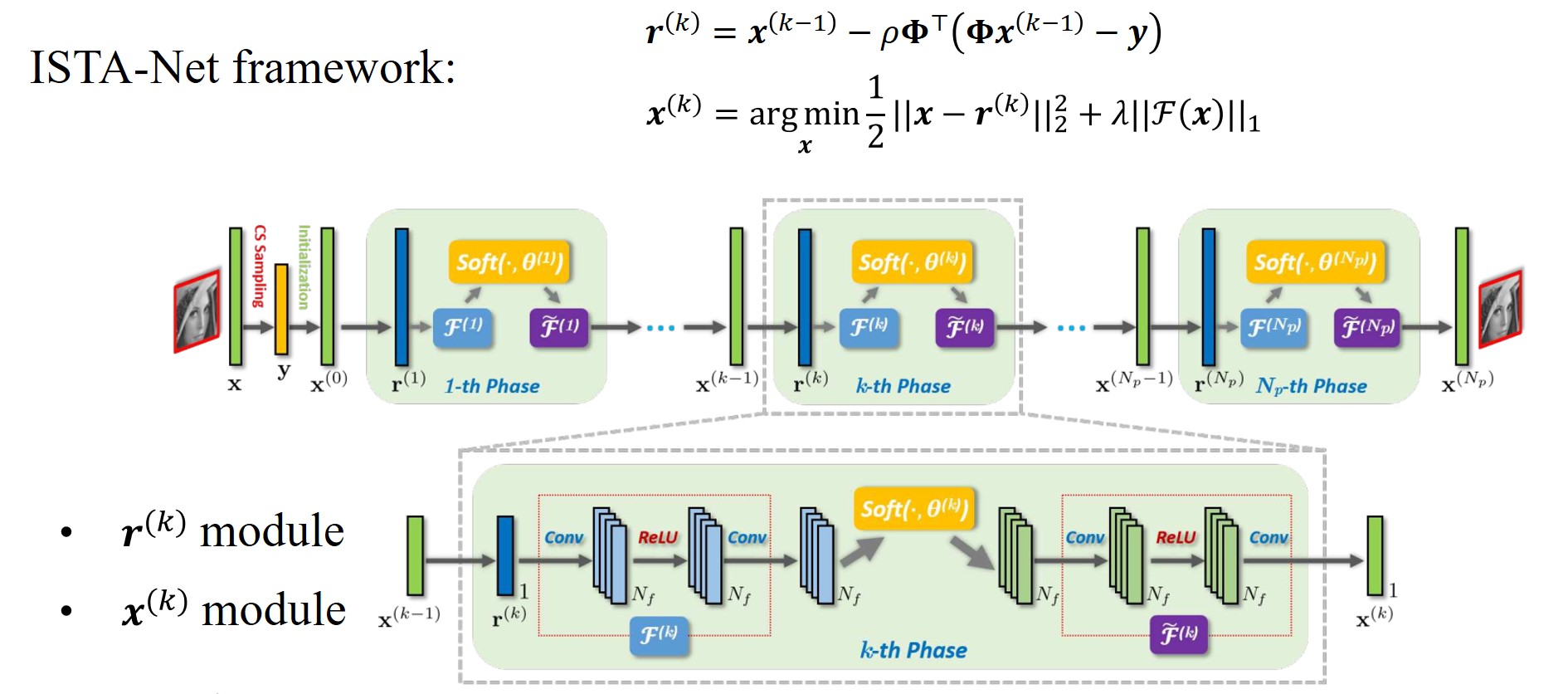
1. ISTA-Net – $\boldsymbol{r}^{(k)}$ Module
为了保持ISTA算法的结构优势,同时增加网络的灵活性,ISTA-Net允许步长参数是可学习的。该模块的更新公式表示如下:
\[\boldsymbol{r}^{(k)}=\boldsymbol{x}^{(k-1)}-\rho^{(k)} \boldsymbol{\Phi}^{\top}\left(\boldsymbol{\Phi} \boldsymbol{x}^{(k-1)}-\boldsymbol{y}\right).\]2. ISTA-Net – $\boldsymbol{x}^{(k)}$ Module
利用定理,可以将优化问题变换为如下形式:
\[\boldsymbol{x}^{(k)}=\underset{\boldsymbol{x}}{\arg \min } \frac{1}{2}\left\|\mathcal{F}(\boldsymbol{x})-\mathcal{F}\left(\boldsymbol{r}^{(k)}\right)\right\|_{2}^{2}+\theta\|\mathcal{F}(\boldsymbol{x})\|_{1}.\]
上述优化问题有闭式解:
\[\mathcal{F}\left(\boldsymbol{x}^{(k)}\right)=\operatorname{soft}\left(\mathcal{F}\left(\boldsymbol{r}^{(k)}\right), \theta\right),\]受小波变换可逆性的启发,$\mathcal{F}(\cdot)$应该满足$\widetilde{\mathcal{F}} \circ \mathcal{F}=I$,则有
\[\boldsymbol{x}^{(k)}=\tilde{\mathcal{F}}\left(\operatorname{soft}\left(\mathcal{F}\left(\boldsymbol{r}^{(k)}\right), \theta\right)\right).\]3. ISTA-Net的可学习参数
ISTA-Net中的可学习参数如下图:
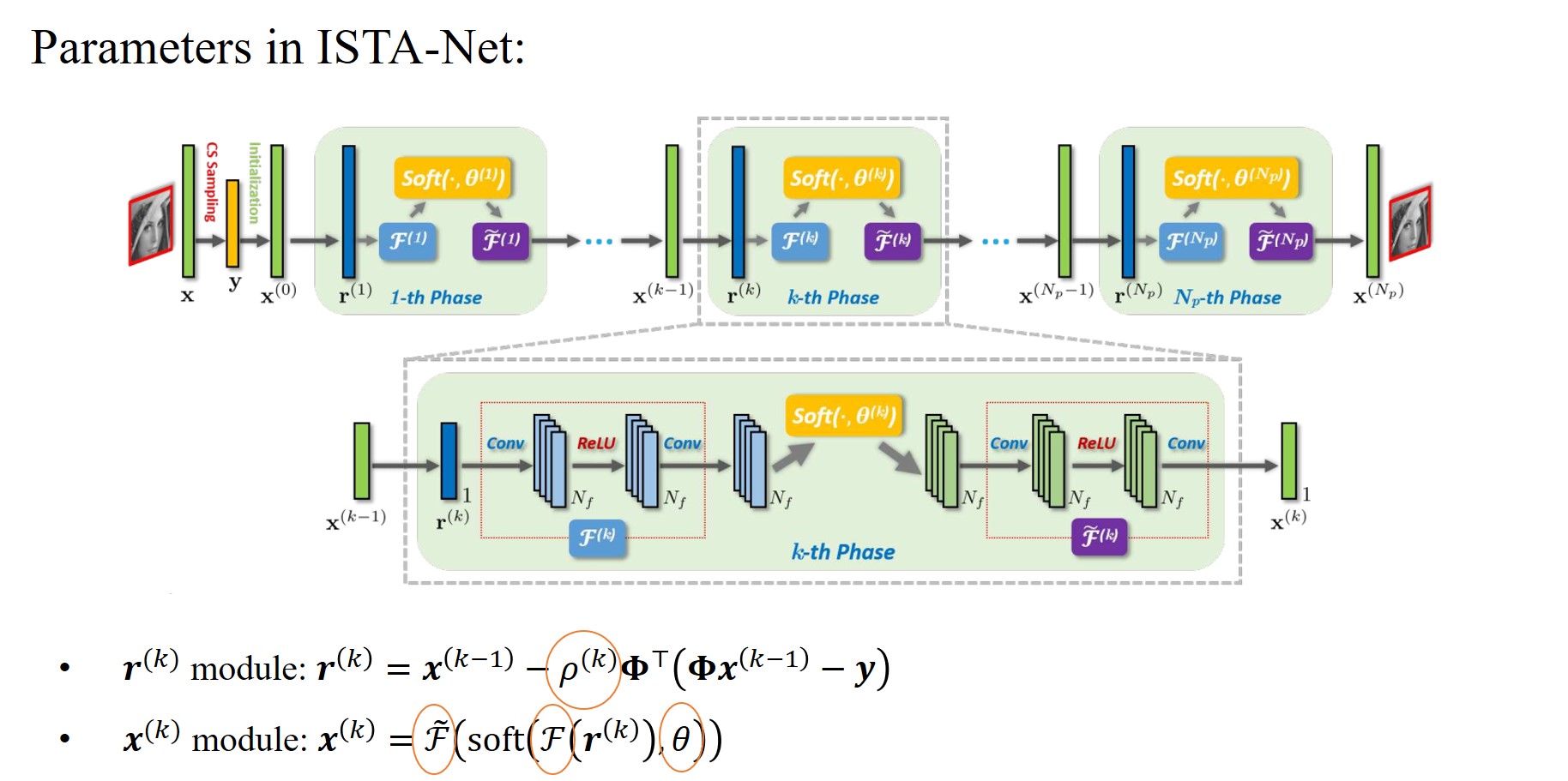
4. ISTA-Net的损失函数设计
ISTA-Net的损失函数包括重建损失和可逆损失,具体表示如下:

5. 增强版本$\text{ISTA-Net}^{+}$
由于自然图像和视频的残差应该是更可压缩的,则可以假设
\[x^{(k)}=\boldsymbol{r}^{(k)}+\boldsymbol{w}^{(k)}+\boldsymbol{e}^{(k)},\]其中$\boldsymbol{e}^{(k)}$表示噪声,$\boldsymbol{w}^{(k)}$表示缺失的高频成分,可以通过线性操作来提取,即
\[\boldsymbol{w}^{(k)}=\mathcal{R}\left(\boldsymbol{x}^{(k)}\right)=\mathcal{G} \circ \mathcal{D}\left(\boldsymbol{x}^{(k)}\right),\]同时建模$\mathcal{F}(\cdot)=\mathcal{H} \circ \mathcal{D}$,则可以通过如下流程求解$\boldsymbol{x}^{(k)}$:
\[\begin{gathered} \min _{\boldsymbol{x}} \frac{1}{2}\left\|\mathcal{H}(\mathcal{D}(\boldsymbol{x}))-\mathcal{H}\left(\mathcal{D}\left(\boldsymbol{r}^{(k)}\right)\right)\right\|_{2}^{2}+\theta\|\mathcal{H}(\mathcal{D}(\boldsymbol{x}))\|_{1} \Rightarrow \boldsymbol{x}^{(k)} \Rightarrow \boldsymbol{x}^{(k)}=\boldsymbol{r}^{(k)}+\mathcal{R}\left(\boldsymbol{x}^{(k)}\right), \\ \boldsymbol{x}^{(k)}=\boldsymbol{r}^{(k)}+\mathcal{G}\left(\tilde{\mathcal{H}}\left(\operatorname{soft}\left(\mathcal{H}\left(\mathcal{D}\left(\boldsymbol{r}^{(k)}\right)\right), \theta\right)\right)\right). \end{gathered}\]$\text{ISTA-Net}^{+}$网络的参数可以总结为:
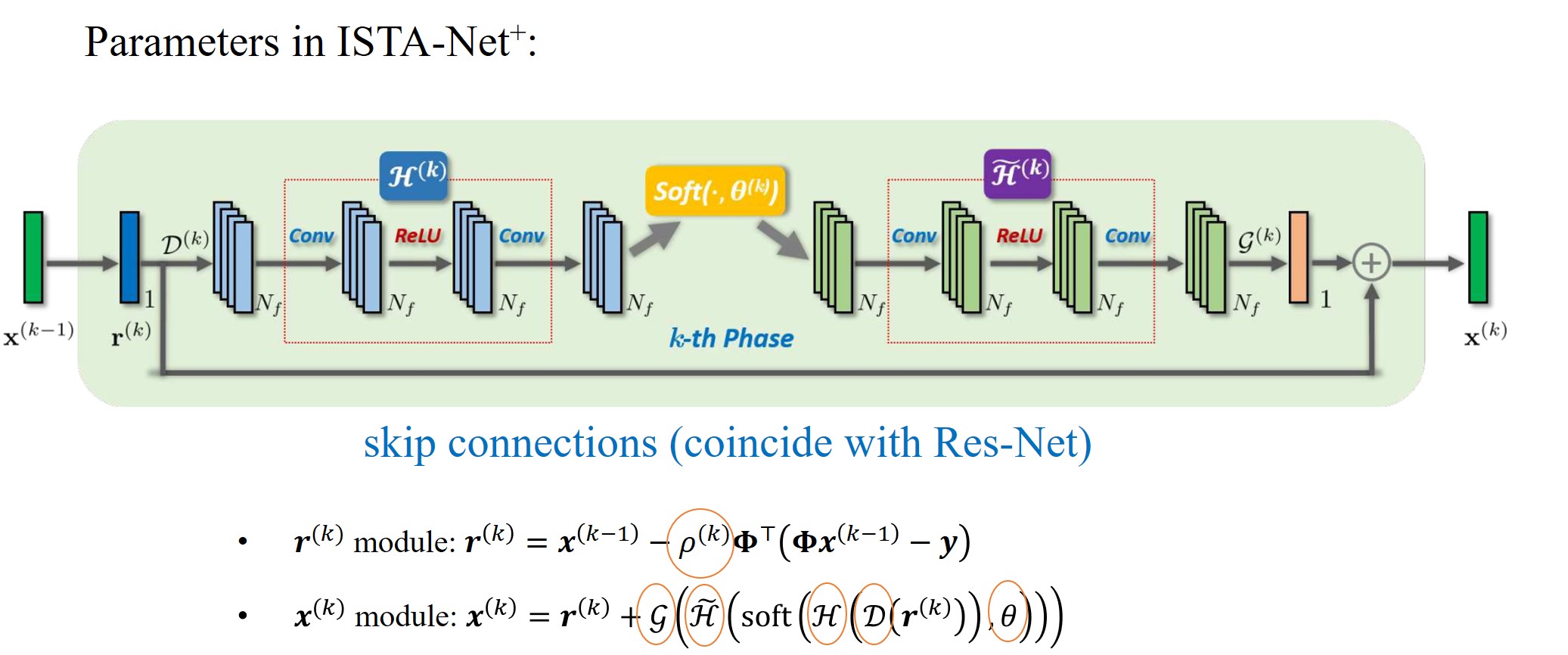
6. 数值实验
ISTA-Net与$\text{ISTA-Met}^{+}$的对比:
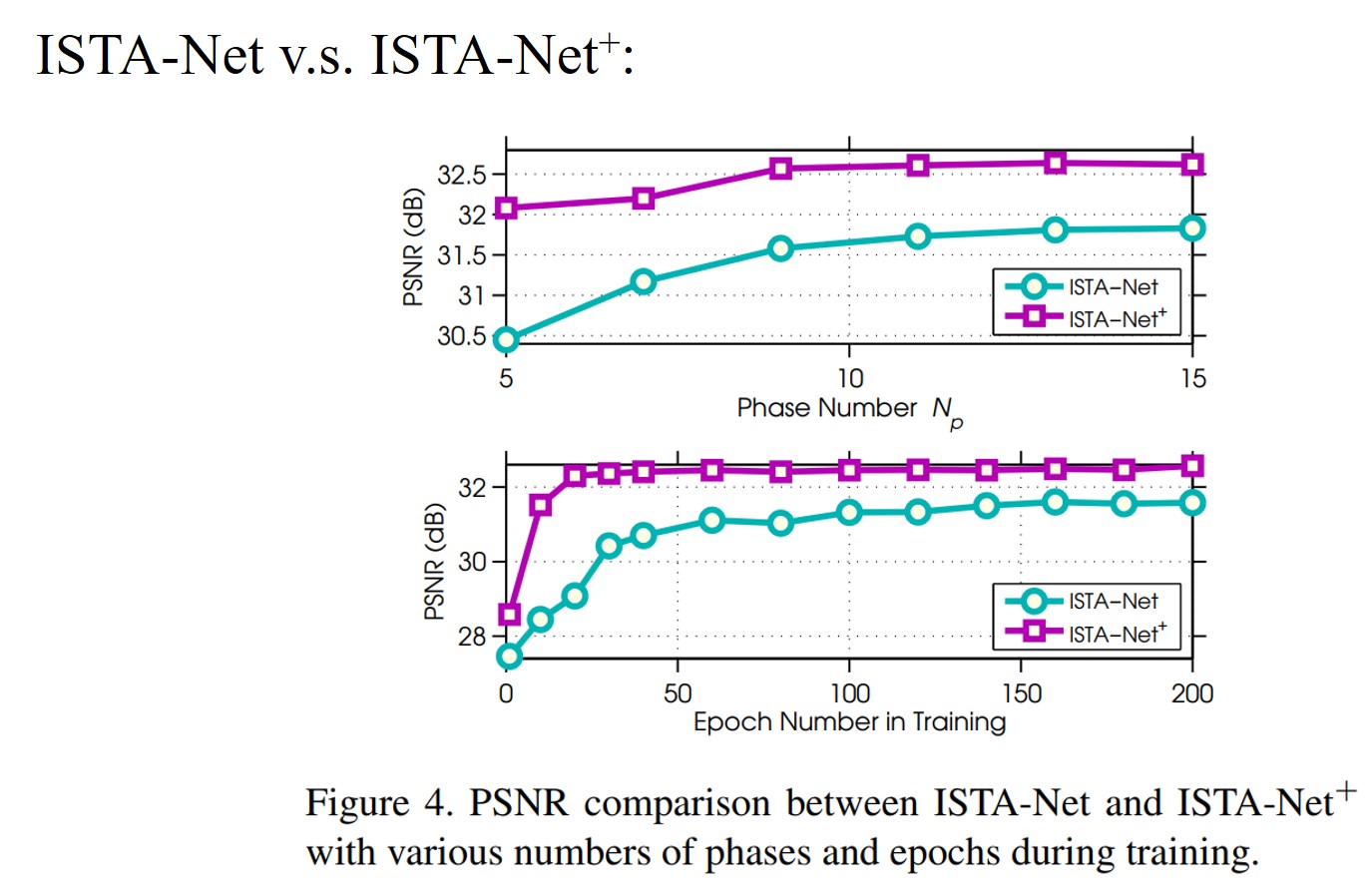
公共数据集实验:
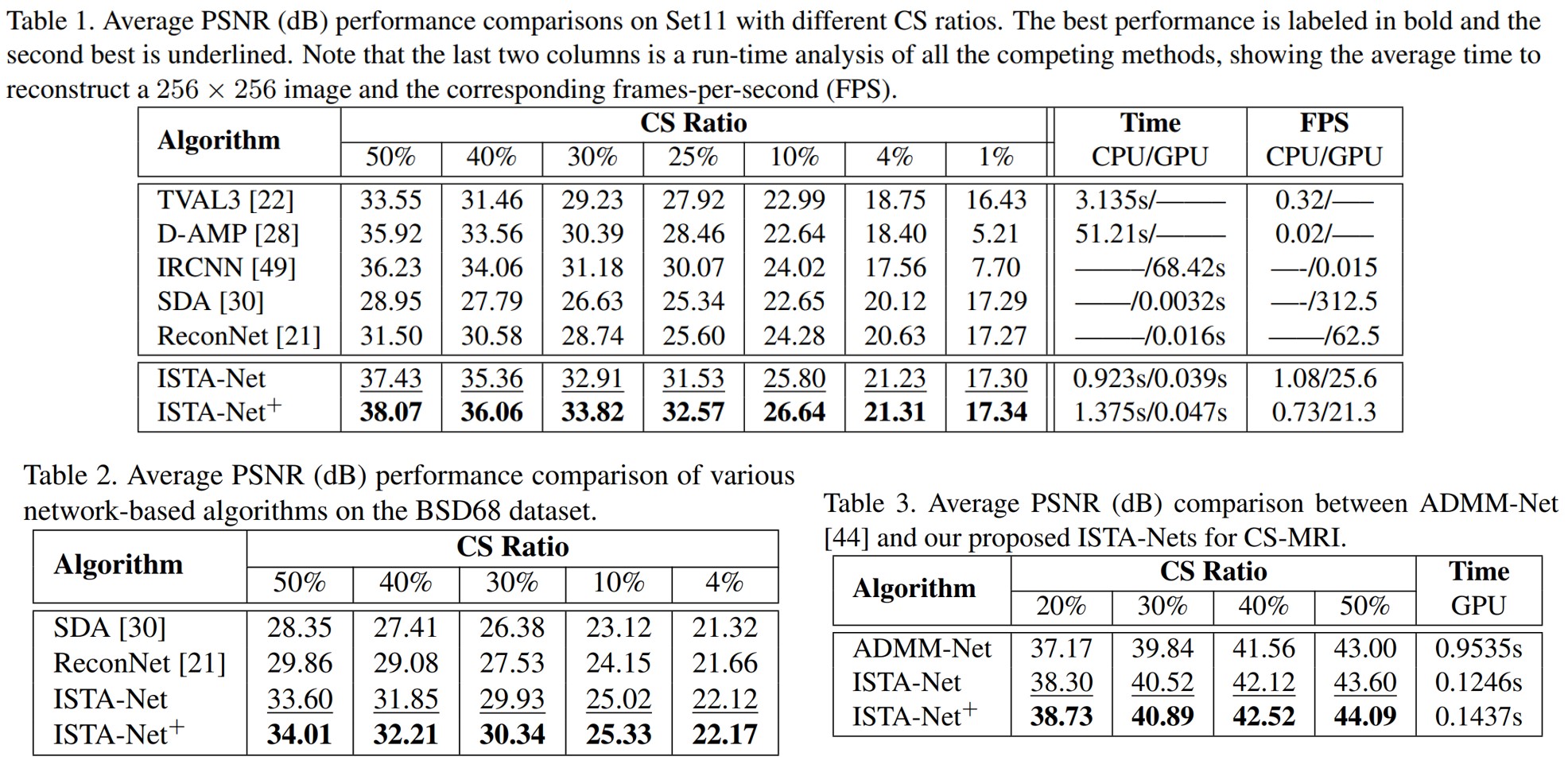
FISTA-Net: Learning A fast iterative shrinkage thresholding network for inverse problems in imaging (2021, TMI)
本文是对ISTA-Net的改进版本,文章中注意到ISTA-Net训练后可能带有非正的步长和阈值参数,这是与传统方法不相契合的。同时,FISTA算法(见参考文献[9])是对ISTA算法的加速版本,引入了动量模块以加快收敛。具体来说,本文的主要贡献总结如下:
在FISTA-Net中,梯度矩阵是通过在整个迭代过程中替换固定的经典梯度来学习的;
FISTA-Net 的核心参数,例如步长、阈值,被正则化以正确收敛;
在FISTA-Net中增加了一个动量模块来加速收敛。
FISTA算法流程与FISTA-Net的对应模块操作总结如下:

1. FISTA-Net – Gradient descent module $\boldsymbol{r}^{(k)}$

2. FISTA-Net – Proximal mapping module $\boldsymbol{x}^{(k)}$
\[\boldsymbol{x}^{(k)}=\mathcal{J}_{\theta^{(k)}}\left(\boldsymbol{r}^{(k)}\right).\]具体实现方式与ISTA-Net类似,利用卷积层+ReLU激活函数拟合,同样带有可逆性约束。
3. FISTA-Net – Momentum module $\boldsymbol{y}^{(k+1)}$
通过引入动量模块加速收敛,表示为: \(\boldsymbol{y}^{(k+1)}=\mathbf{x}^{(k)}+\rho^{(k)}\left(\boldsymbol{x}^{(k)}-\boldsymbol{x}^{(k-1)}\right).\)
4. FISTA-Net – Parameter constraints
ISTA-Net 在迭代过程中可能会生成非正的步长和阈值,这与这些变量的定义相矛盾。所以在本文提出的FISTA-Net中引入了正则化约束,保证步长参数是非负的,即
\[\begin{aligned} \mu^{(k)} &=s p\left(w_{1} k+c_{1}\right), w_{1}<0, \\ \theta^{(k)} &=\operatorname{sp}\left(w_{2} k+c_{2}\right), w_{2}<0, \\ \rho^{(k)} &=\frac{\operatorname{sp}\left(w_{3} k+c_{3}\right)-s p\left(w_{3}+c_{3}\right)}{s p\left(w_{3} k+c_{3}\right)}, w_{3}>0, \end{aligned}\]其中$\operatorname{sp}(\cdot)$为softplus函数,即$\operatorname{sp}(x)=\ln (1+\exp (x))$,且$\rho^{(k)} \in(0,1)$。
5. FISTA-Net的框架
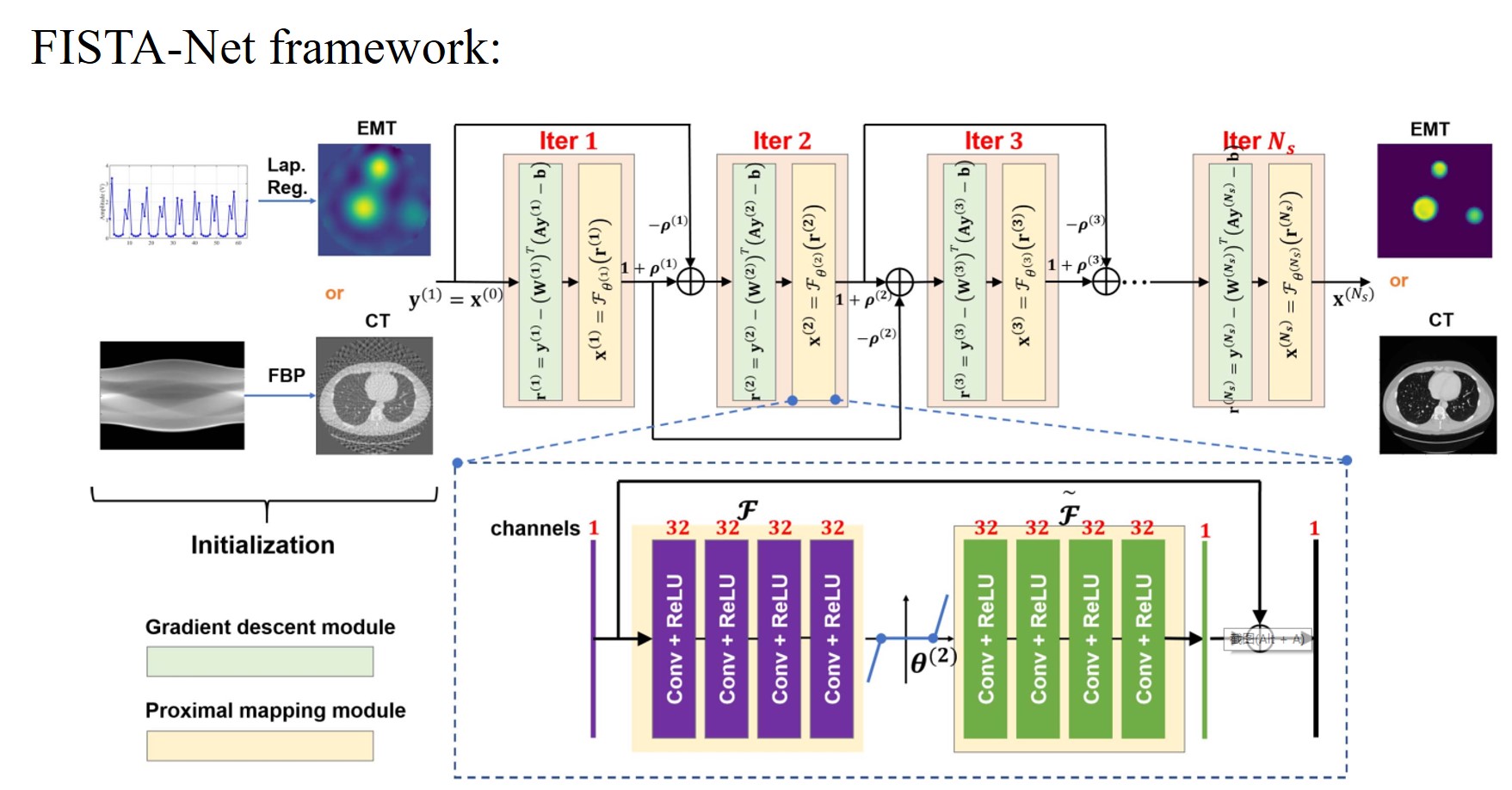
5. FISTA-Net的损失函数
FISTA-Net的损失函数由重构mse损失,可逆性损失和稀疏损失组成,表示为:
\[\begin{aligned} &\mathcal{L}_{\text {total }}=\mathcal{L}_{\text {mse }}+\lambda_{1} \mathcal{L}_{\text {sym }}+\lambda_{2} \mathcal{L}_{\text {spa }}\\ &\text { with }\left\{\begin{array}{l} \mathcal{L}_{\mathrm{mse}}=\left\|\boldsymbol{x}_{N_{s}}-\boldsymbol{x}_{g t}\right\|_{2}^{2} \\ \mathcal{L}_{\mathrm{tsf}}=\lambda_{1} \mathcal{L}_{\mathrm{sym}}+\lambda_{2} \mathcal{L}_{\mathrm{spa}} \end{array}\right.\\ &=\lambda_{1} \sum_{k=1}^{N_{S}}\left\|\tilde{\mathcal{F}}\left(\mathcal{F}\left(\boldsymbol{r}^{(k)}\right)\right)-\boldsymbol{r}^{(k)}\right\|_{2}^{2}+\lambda_{2} \sum_{k=1}^{N_{S}}\left\|\mathcal{F}\left(\boldsymbol{r}^{(k)}\right)\right\|_{1}. \end{aligned}\]6. FISTA-Net的实验展示
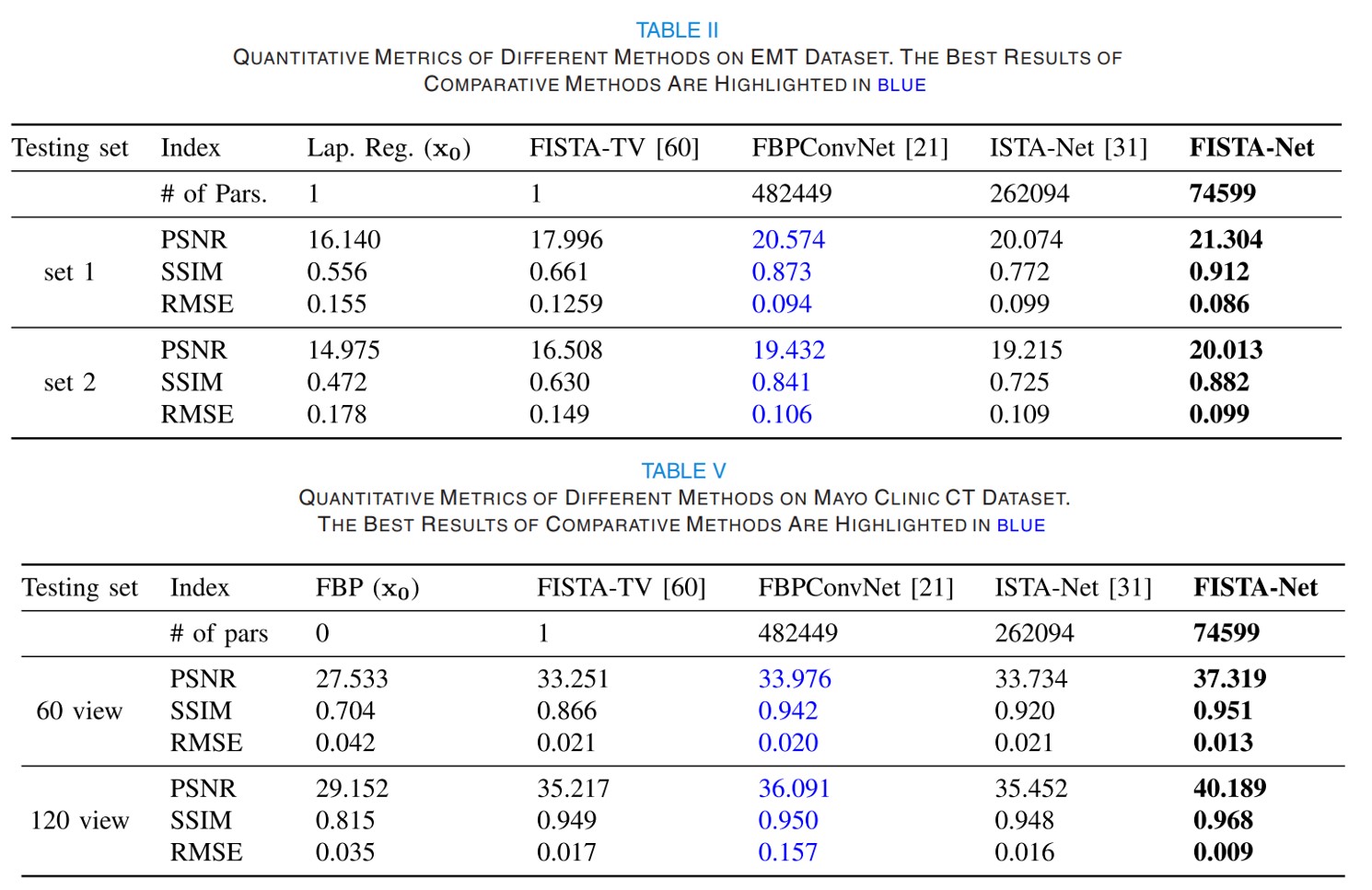
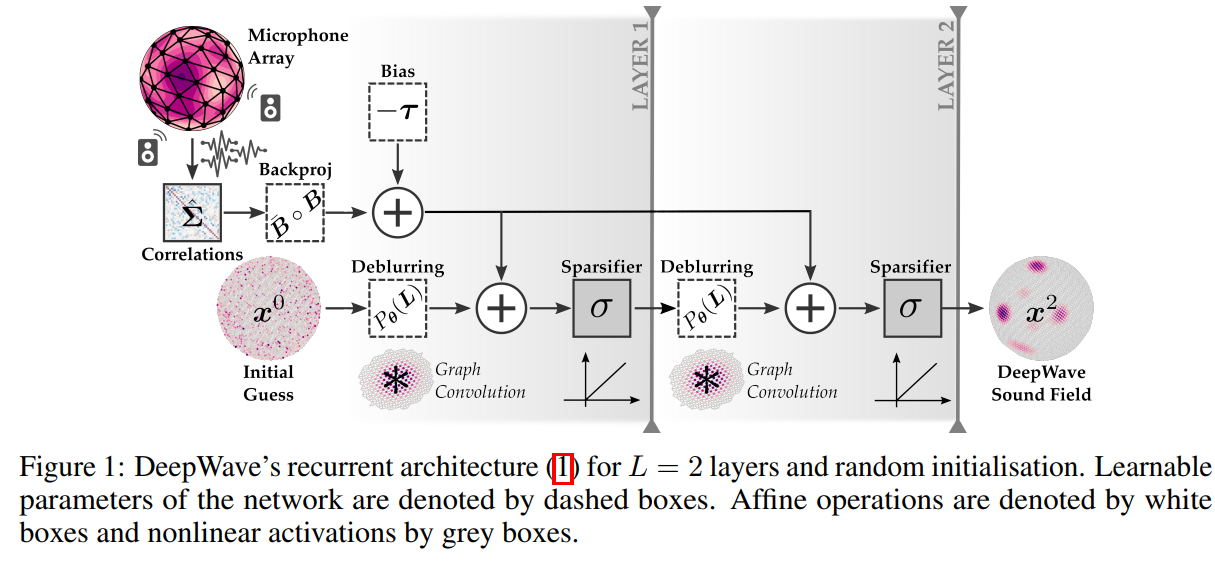
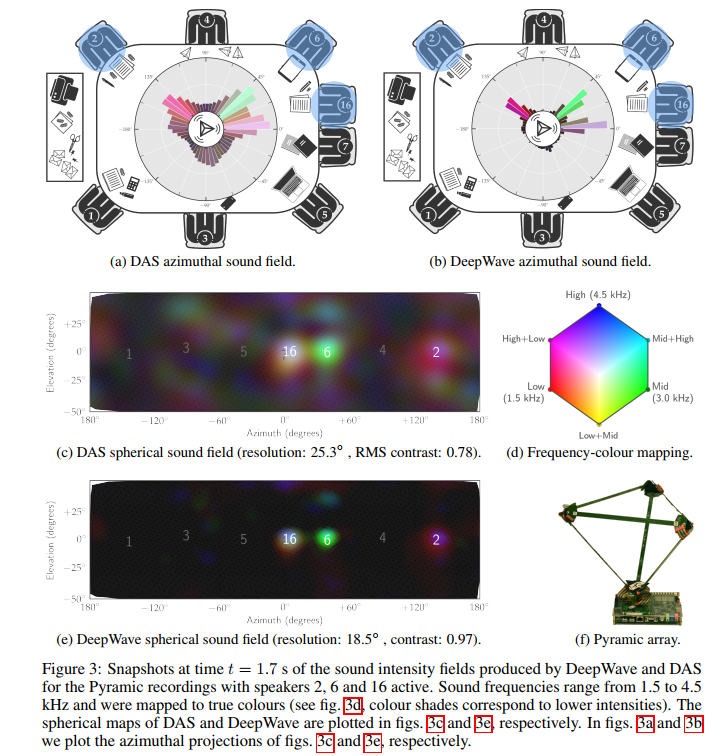
DeepWave: a recurrent neural-network for real-time acoustic imaging (2019, NIPS)
DeepWave是专门为三维声成像设计的模型驱动的深度网络。具体来说,DeepWave是将声学成像中的近端梯度下降法展开为一个固定深度的循环网络,同时利用相关定理将参数简约化。DeepWave可以很好地达到时间和分辨率性能的平衡,在满足实时成像的同时,拥有不错的分辨率。网络结构和部分实验结果展示如下,具体实现过程在此不做详述(懒)。